#. 6 Tree

자료구조

#. 6 Tree

Haksae 2022. 3. 14. 11:22

1. 트리와 용어 정리

트리(Tree)는 그래프의 일종으로, 노드들이 나무가지처럼 연결된 비선형 계층적 자료구조이다.
트리는 데이터 구조의 계층적인, 상하 관계 속성을 표현한다.
- 선형적 자료구조는 데이터의 이전 데이터나 다음 데이터의 순서가 존재했다.
- 트리도 내부적으로 순서 정보를 가지도록 구현할 수 있지만, 트리라는 자료구조 자체에서 데이터의 순서는 그리 중요한 요소가 아니다.

* Tree와 관련된 용어 정리
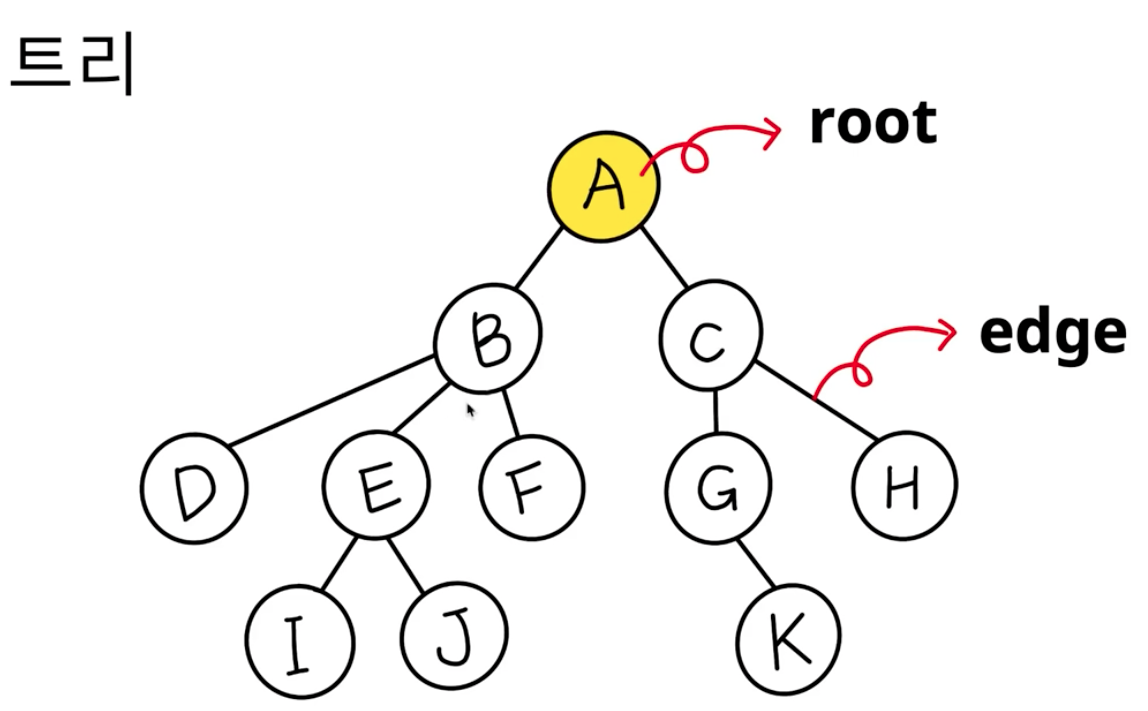
- 루트 노드(root node): 부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.
- 단말 노드(leaf node): 자식이 없는 노드, ‘말단 노드’ 또는 ‘잎 노드’라고도 부른다.
- 내부(internal) 노드: 단말 노드가 아닌 노드
- 간선(edge): 노드를 연결하는 선 (link, branch 라고도 부름)
- 형제(sibling): 같은 부모를 가지는 노드
- 노드의 크기(size): 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이(depth): 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- 노드의 레벨(level): 트리의 특정 깊이를 가지는 노드의 집합
- 노드의 차수(degree): 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
- 트리의 차수(degree of tree): 트리의 최대 차수
- 트리의 높이(height): 루트 노드에서 가장 깊숙히 있는 노드의 깊이

2. 트리의 특징

트리는 DAG(Directed Acyclic Graphs, 방향성이 있는 비순환 그래프)의 한 종류이다.
- loop나 circuit, self-loop도 없다.
- 트리는 사이클이 없는 하나의 연결 그래프다. (Connected Graph)
노드가 N개인 트리는 항상 N-1개의 간선(edge)을 가진다.
- 즉, 간선은 항상 (정점의 개수 - 1) 만큼을 가진다.
루트에서 어떤 노드로 가는 경로는 유일하다.
- 임의의 두 노드 간의 경로도 유일하다. 즉, 두 개의 정점 사이에 반드시 1개의 경로만을 가진다.
한 개의 루트 노드만이 존재하며 모든 자식 노드는 한 개의 부모 노드만을 가진다.
- 부모-자식 관계이므로 흐름은 top-bottom 아니면 bottom-top으로 이루어진다.
순회는 Pre-order, In-order 아니면 Post-order로 이루어진다. 이 3가지 모두 DFS/BFS 안에 있다.